- Leakage of Light in Diamonds and Its Estimation
- Stereoview: Stereovision and evaluation of leakage
- Taking into account the features of human perception
- Brilliance
- Light Return
- Contrast
Leakage of Light in Diamonds and Its Estimation
In a diamond, there are some regions that do not return light towards the observer's eye. If we trace those rays connecting the eye with the regions that show no brilliance, we'll find out that some of these rays leave the diamond through its crown but do not propagate towards the source of illumination. Another portion of these rays leaves the diamond through its pavilion, giving rise to the phenomenon called leakage. The third portion of these rays becomes screened by the observer's head or body, giving rise to the effect known as NailHead.
All the three effects cause the observer to see dark, non-illuminated regions in the diamond. Analyzing the leakage and the NailHead effect allows one to reveal such regions of the diamond, which are dark regardless of the type of illumination. It is especially important to determine the parameters of the diamond, for which these dark regions combine into large zones. In such a case, the observer easily notices an abrupt decrease in the local contrast.
It is possible to observe the regions of leakage by placing the diamond into a Firescope that illuminates the stone with white light from the side of its pavilion.
 |
 |
| Photo made with the Firescope |
Model of the same diamond, using illumination of the Firescope type |
White regions can be seen here and there. Therefore, a light ray passes through these regions from under the diamond to the observer's eye. If such a diamond was mounted into a jewel, we would see the mounting through these regions and would never see any light originating from the illumination source. Therefore, the more leakage regions the diamond contains (and the stronger the leakage effect), the fewer the regions of the diamond, capable of reflecting the illumination into the observer's eye, and the worse the cut quality of the stone.
Theoretically, it is possible to imagine such a location of the illumination source, from which a light ray enters the diamond and splits into multiple rays there, some of these leaving the diamond towards the observer's eye. However, these rays can be only secondary (not primary) ones, which are either quenched due to polishing or become so weak upon leaving the stone that the observer will not perceive them as bright light.
 |
 |
| Ray path from the eye, which leads to leakage through the pavilion |
Return path of a primary ray having the same trajectory |
Besides the white regions, it is possible to notice some gray regions in the stone observed. These regions show partial leakage of light. In other words, some rays leave the diamond through its pavilion, while the other ones leave it through the crown. If a ray originating from the illumination source passes through such a region, the partial leakage attenuates the ray and only a portion of the original ray reaches the observer's eye. This can be demonstrated by tracing the ray as it passes through the white and gray regions:
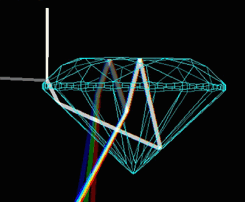 |
 |
| Ray path through a white region |
Ray path through a gray region |
To reveal those dark regions caused by light leakage, that is, the regions, which remain dark upon arbitrary daylight illumination of a collet-set stone a model of Leakage-type illumination has been built. The model is a hemisphere located below the pavilion of the diamond and extends up to the girdle plane (upper edge of the girdle). Thus, the model takes into account those rays leaving the stone through its pavilion or girdle.
Those zones of the diamond looking bright upon the Leakage-type illumination will be dark upon usual illumination.
To some extent, this kind of illumination is similar to the illumination from below, used in the Firescope. The main difference between these is the fact that the Leakage-type illumination reveals only light leakage. Therefore, those regions of the stone looking pink under the Firescope illumination are gray under the Leakage-type illumination.
 |
 |
| Firescope-type illumination |
Leakage-type illumination |
In order to analyze the cut quality of the diamond and the accuracy of its proportions, it is reasonable to quantitatively estimate the leakage of light. We propose the following way of doing that. The leakage is estimated as the subjective brightness of light that returns to the observer's eye in the case when the illumination of the diamond is of the Leakage type. Here we use a model of photo objective (diameter 150 mm, distance to diamond 60 cm) as a viewer. Here we not take into account human stereoview. We suggest calling this viewer a "Photoreceptor".
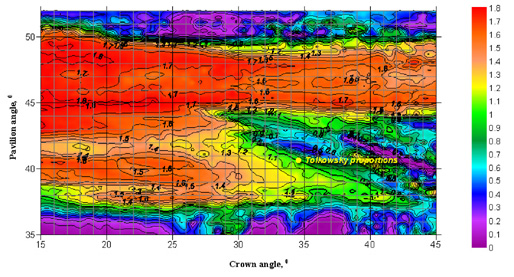
Since there are some stones that show considerable leakage primarily through the table, we calculated two leakage types: through the whole crown of the diamond (plot 1) and through the table solely (plot 2). Those portions of the plots characterized by large leakage values represent undesirable proportions of the stone, that is, those cut parameters causing considerable leakage of light either through the crown or through the table.
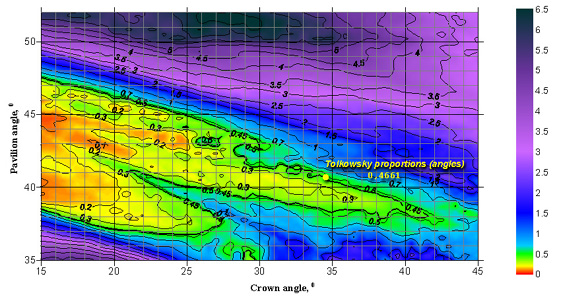 |
| Plot 1. Light leakage through the crown of a round brilliant cut diamond with a table spread of 57% and a girdle thickness of 1% as a function of the crown angle and the pavilion angle. The distance between the photoreceptor and the diamond is 60 cm. The plot is based on the image observed by photoreceptor. The diamond is oriented so that the table looks towards the observer. The larger the leakage value plotted, the stronger the leakage effect and the lower the quality of the diamond. |
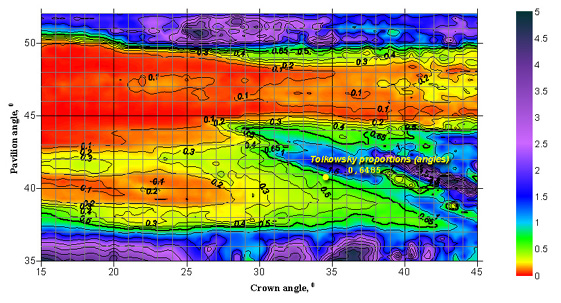 |
| Plot 2. Light leakage through the table of a round brilliant cut diamond with a table spread of 57% and a girdle thickness of 1% as a function of the crown angle and the pavilion angle. The distance between the photoreceptor and the diamond is 60 cm. The plot is based on the image observed by the photoreceptor. The diamond is oriented so that the table looks towards the observer. The larger the leakage value plotted, the stronger the leakage effect and the lower the quality of the diamond. |
When analyzing these plots, it turns out that they are quite similar to plots of diamond's Light Return. This fact is absolutely reasonable, because the Light Return through the crown and the light leakage through the pavilion should be interrelated. At the same time, some differences can be noticed, the most interesting one corresponding to the region close to the Tolkowsky's cut parameters (slightly upper on the plot than these). This region looks good from the point of view of Light Return but much worse from the point of view of light leakage. When studying gems belonging to this cut parameter range, one can notice that their Light Return is high only in the «crown looks to the observer» position. When swinging such a stone, its Light Return appears to be lower than that of a diamond cut in accordance with the Tolkowsky's parameters.
When studying the effect of light leakage, an inversion function was introduced, which is required to adequately take into account the leakage during the geometric averaging. So, the stronger the leakage, the smaller the leakage measure supplied to the averaging procedure. Only in this case the geometrical averaging will cull out those stones showing strong leakage of light. Another purpose of using the inversion function is correct normalization of the leakage value with respect to the Tolkowsky's cut parameters. The leakage value for these parameters should be 1. Otherwise, a mismatch arises between modeling light return and other effects, violating the resultant brilliance function that takes into account both the brilliance and effects.
We propose to refer to the value of leakage, obtained with the use of the subjective grading and inversion functions, as the adapted leakage.
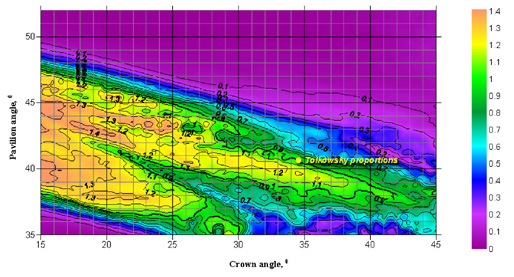 |
| Plot 3. Adapted leakage calculated for the table of a round brilliant cut diamond with a table spread of 57%. The position of the stone is static; photoreceptor. |
 |
| Plot 4. Adapted leakage calculated for the crown of a round brilliant cut diamond with a table spread of 57%. The position of the stone is static; photoreceptor. |
|




















